Spelunking Problem

Introduction

The spelunking problem deals with the idea of finding a spelunker who has become lost in a system of caves and focuses on determine what is the minimum number of searchers needed to find the lost spelunker regardless of how he behaves. A cave can be regarded as a collection of sets of pathways and intersections, so it can be modeled as a graph with the pathways being labeled as edges and the intersections labeled as vertices. Here is an example of modeling a Regina map as a graph.

Usually there are two ways to search graphs - searching just the vertices or searching each of the edges. In my post, I will focus on searching the edges of the graphs. Searching the edges of the graphs means the searchers will move along the different corridors making sure that the lost spelunker is not anywhere in that corridor. However, as you may think of, sometimes the lost spelunker may be wandering around inside the caves and not just standing in a stationary position. Under such situation, in order to make sure the lost spelunker cannot unknowingly circle back behind them and go back into a corridor they have already searched, the searches occasionally have to leave searchers at vertices in a stationary spot.

Terminology

Blockers: searchers who will stay stationary at one vertex.

Search plan: 

If the formal definition is hard to follow, you can just think of e(t) and f_i(t) as the positions at time t of a lost spelunker and the ith searcher. Then a search plan must catch the lost spelunker in a finite time.

Search number: denote s(G), is the minimum cardinality of all search plans for a graph G.
Note: the search number in the spelunking Problem can be regarded as capture time in general.
Tree: an undirected graph in which any two vertices are connected by exactly on path.
Twig: a twig of a connected graph G is an edge whose ends has degree 1 in G.

Searching Methods

There are two searching methods that always be used, one-tick searching and two-tick searching. One-tick searching means each searcher is allowed to move at most once and searchers can begin at any vertex. Two-tick searching means each searcher is allowed to move at most twice and searchers can begin at any vertex, but can move down only two edges at most.
Let us consider C_4, a circular graph with 4 vertices. In this case, we need 4 searchers to search it when apply the one-tick searching. But we don't need any blockers in this case. The example is shown below:

The numbers labeled represents the searchers, the edge labeled with the number 1 indicates searcher number a moves along the edge and a number 2 indicates searcher number 2 moves along that edge, etc. In general, one-tick searching is the fastest way to search graphs, since all searchers can move simultaneously and search the entire graphs at once. However, the disadvantage of this method is it requires a lot of searchers, especially for large graphs. So this method is not always feasible.

Now let us move to two-tick searching and again, we will look at C_4 graph. In this example, the colors indicate the order of the moves. Red is the first move and blue is the second. The numbers indicate the searchers as it is in the one-tick searching, an edge labeled with number 1 indicates searcher number 1 moves along that edge and number 2 indicates searcher number 2 moves along that edge. So the colored graph would looks like the following:

So under the assumption that both searchers can move at the same time, the spelunker could be found in at least two moves. And by the time the two searchers meet they would have found the lost spelunker with absolute certainty.

Search Number of A Connected Graph

In order to be consistent and easy to understand, let us assume the cave can be regarded as a finite connected graph in which the searchers and the lost spelunker must move continuously. Let G be a finite connected graph without loops or multiple edges. Then search number s(G) <= n+1, where n is the number of vertices of G. Understanding the terminology "blockers" will provide us with an easier way to explain why s(G) <= n+1. We can set a blocker at each vertex in G, then there are total of n blockers. So we only need an additional searcher follows any path which traverses every edge of G and thus acquire the search number s(G) <= n+1.
I found several examples that will help us to gain insight into the nature of s(G), and I will go over some of them in class on Tuesday since I don't know how to draw a graph in the blogger and it would be too abstruse without having a graph. So let us do it on Tuesday!

Search Numbers of Trees

After we get a general understanding of search number, let's move to our final goal--characterize s(T) for all trees T. 

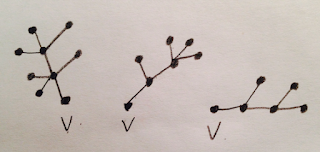
First, let us understand what is a branch. If v is a vertex of tree T, a branch of T at v is a maximal subtree T' of T such that v is a vertex of degree 1 in T'. Below is an intuitive example

Figure 1

Figure 2

Figure 1 is a tree graph T and Figure 2 represents the branches of T at vertex v.

Theorem 2:

Let k >= 1, and T be a tree. Then s(T) >= k+1 if and only if T has a vertex v at which there are at least three branches T_1, T_2, T_3 satisfying s(T_j) >= k for j=1, 2, 3.

This theorem can be used to characterize all trees with a given search number. Before we attempt to prove this theorem, we should understand Lemma 4 and Theorem 1 since they need to be used while we prove theorem 2.

Lemma 4:

Let T_1, T_2, T_3 be disjoint trees each having at least one edge. For j = 1, 2, 3 let v_j be a vertex of degree 1 in T_j. Let T be the tree obtained by identifying v_1, v_2, v_3 into a single vertex v. If s(T_j)=k for j=1, 2, 3, then s(T)=k+1.

Theorem 1:

If H is a connected subgraph of G, then s(H) <= s(G).

Preceding stuff:

If T is a tree with s(G)=k, then for each integer r with 1 <= r <= k, T has a subtree T' such that s(T')=r.

Now let us do a simple proof of the forward direction of Theorem 2.

Proof:  Suppose T has a vertex v with branches T_1, T_2, T_3 such that s(T_j) >= k.

            Then v is of degree 1 in each T_j by the definition of branches.

            By the preceding stuff, we  know that T_j has a subtree T'_j with s(T'_j)=k in which v has degree of 1.

            The subtree T' spanned by T'_1, T'_2, T'_3 has s(T')=k+1 by Lemma 4.

            Therefore, s(T) >= k+1 by theorem 1.

For determining search number of trees, there are tons of proofs we can look at. Since our goal is to get a general understanding of spelunking problem, so I think this is a good place to stop. But I will go over the proof of Theorem 2 in class on Tuesday.

Final Thoughts

The spelunking problem is a very interesting topic that definitely worth exploring. There are many variations of this searching problem such as the searchers can radio each other to modify their search plan to incorporate the new information. And variations even exist in higher dimensions. But as deep as we explore this problem, the more Graph Theory knowledge will be required. So if you doesn't feel comfortable with all the proofs or terminologies mentioned above thats fine! We'll go over them together in class on Tuesday and hope everyone can at least get to know how this "game" be set and played by then.

Reference

T. D. Parsons. "Pursuit-Evasion in a Graph".

Selinger C. "Spelunking Problem: how the solution works".