Cop vs. Drunk

It's another standard night on St. Lawrence campus: someone has just knocked down all the exit signs in Sykes again, and a security guard is on her way to impart justice to the vandal. The culprit knows the dorm layout just as well as security and can run just as fast. Good thing he's absolutely hammered.

Even sober people get lost in these halls.

Variant of Cops & Robbers: Cop vs. Drunk

Our game of Cop vs. Robber plays the same except the robber is drunk and is unable to chose what to do on each of his turns. Rather, he must move from vertex to vertex using a random walk. He picks one of the paths available to him to move down randomly such that each path has an equal probability of being chosen.Given some graphs, one can easily figure out the maximum length for how long a cop is going to take to capture the drunk. A path graph would allow the cop to start in the middle and, in a worse-case-scenario, travel half the path to an end point to catch the drunk. In a complete graph, one where every vertex is adjacent to every other vertex, would allow the cop to catch the drunk in no more than one turn. However, not all graphs are so easy, we might care more about the expected catch time rather than the maximum catch time, and there are different strategies that the cop can use to choose which path to take to the drunk. We can use some known facts to get the simple examples out of the way.

Lazy Cop

What if the cop doesn't try? The cop can move back and forth between two points, or be forced to stay on one vertex, letting the drunk move around with no pursuer. The cop will still always win since the drunk will, eventually, randomly stumble into the cop. The maximum possible expected hitting time, the time expected to visit every vertex on a graph at least once, for a random walk on the worst possible graph is $4n^3/27$ + lower order terms. As such, we can expect the the lazy cop to catch the drunk in, at most, this many moves. Unless the cop is activity avoiding the drunk, the cop will always win.

Path Graph

Living life on the straight and narrow has its benefits for the cop.

Suppose the cop is pursuing the drunk on a path graph, a graph that has vertices with a single connected path that connects all of them, with n vertices. A random walk on a path will, on average, move $\sqrt{t}$ distance in $t$ time. So, if a cop starts in at one end of the graph and the drunk starts at the other, the drunk will move expected $\sqrt{t}$ toward the cop while the cop moves t toward the drunk. So, the capture time is expected to take $n - \sqrt{n}$ turns.

Complete Balanced Bipartite Graph

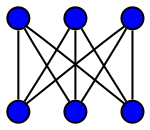A Complete Balanced Bipartite Graph. Known for its interesting applications in graph theory
and a deceptively frustrating puzzle involving buildings and utilities.

Suppose the cop is pursuing the drunk on a complete balanced bipartite graph, a graph with two equally sized disjoint sets of non-adjacent vertices such that each vertex from both sets is adjacent to all the vertices of the other set. It matters little where the cop starts, but the drunk, not wanting to start adjacent to the cop, starts in the same set. Then the cop will only be able to move to the wrong set each turn. The only way she will win is when the drunk moves to her spot by chance. The probability of this happening occurs with probability $2/n$, the total chase is expected to take $n/2$ turns.

Cop personality: Greedy

So far, we've dealt with a greedy cop, one that minimizes her distance to the drunk at each move. Most of the time, this serves us well since the drunk always has a chance to accidentally move toward the cop on some turn, ensuring that the cop gains ground. Consider a tree graph, a graph in which any two vertices are connected by exactly one path. If a greedy cop is pursuing the drunk on a tree graph, the cop will always shorten the distance between the two and, since there is only one path between where the cop is and where the drunk is, the cop is safe from covering the same edge twice, which wastes time. However, graphs exist that would give a greedy cop a much more difficult time.

The Ladder to the Basement

A ladder graph. For the ladder to the basement graph, pretend the lowermost rung is an entire bipartite graph.

Consider the ladder graph, a graph of two path graphs with adjacent corresponding vertices, but with the last rung of the ladder replaced with the basement, a complete balanced bipartite graph. Let half of the vertices be in the ladder portion while the other half are in the basement. Also, let the cop start in the top of the ladder while the drunk starts in the basement. The basement only has two vertices adjacent to the ladder compared to the $n/2 - 2$ other vertices not adjacent to the ladder. So, the drunk has a very high chance of simply flipping between the left and right side of the basement, or left and right sets of the bipartite graph, on each of his turns. The cop, being greedy at the top of the ladder, switches sides each turn to match the drunk, repeating herself over and over until the drunk, by a small chance, finds his way out of the basement. It takes $n/4$ moves for the drunk to leave the basement, and thus not switch sides, on average. Each time the drunk happens to not switch sides, which is much more likely in the ladder than in the basement, the cop will be able to avoid switching sides and move down the ladder toward the drunk. The capture takes an average of $(n/4)^2/2$ steps, which isn't fast.

Cop Personality: Intuition

Clearly, we need a smarter cop. Were a non-algorithmic player controlling the cop, the cop would be able to move down the ladder earlier at the very least. The problem with the greedy cop is that she "re-targets" too often. Because the drunk switched sides, she was forced to switch sides too, wasting a move. One solution would be to keep the drunk's initial position as the cop's target and move towards that point for several turns, then looking to where the drunk is and reassigning the target vertex. There is a four stage process using this new algorithm that offers a faster method of capture.

Stage 1: Cop moves to drunk's initial position. Time taken for this stage is less than the diameter of the graph, which is less than or equal to $n - \Delta + 1$
Stage 2: Cop moves to drunk's position at the end of stage 1. Time taken = $o(n)$.
Stage 3: Cop updates her target vertex every four steps. This stage ends when the cop is no more than distance 3 from the drunk. Time taken = $o(n)$.
Stage 4: Cop becomes greedy and follows the drunk, waiting until he eventually makes a move toward the cop. Time taken = $\Delta$
Total expected time for all stages is $n + o(n)$.

Note: $\Delta$ = maximum degree of a graph, where degree is the number of edges indecent to a vertex.

An Aside: Understanding o(n) and O(n)

The Big-O and Little-o notation are used to describe upper bounds. For cop vs. robber, it is used to describe an upper bound on the capture time. If a bound is described to be $o(n)$, that means the actual function, which may or may not be known, that describes some phenomenon grows slower than $n$ does. For example, if a certain bacteria grew at a rate of $t^2 + t + 500$, we could say that the growth rate was $o(t^3)$, seeing as the actual growth increases slower than $t^3$. This notation is useful when we can know or prove an upper bound on something but not the actual, true function that describes the scenario. Big-O is similar, but instead of giving an upper bound that is strictly greater than the truth, Big-O gives a greater than or equal to bound.

Conclusion

So, we have the greedy algorithm, which is guaranteed to catch the drunk, and the four stage intuition algorithm which can be much faster. Can you come up with another algorithm that could be faster than the greedy cop? Don't think that this challenge is too hard. Assuming, of course, you haven't been drinking.

References

Capturing the Drunk Robber on a Graph by Komarov and Winkler