Red-Blue Hackenbush
If you enjoy taking the chainsaw to the shrubbery, then Hack-en-bush is the game for you. Hackenbush is a combinatorial game. The game-board is preset, containing red and blue lines connected at vertices. All of these lines are somehow connected to the ground/bottom of the paper. There are numerous different playing-boards to choose from, an example of one playing-board is the Hackenbush girl depicted below in Figure 1. Players alternate removing lines. The Right player is allowed to remove only red lines, the Left player is allowed to remove on blue lines (Right=Red, Left=bLue). Once a line is removed, all of the lines above the removed line, not connect to the ground will be erased. For example, in Figure 1, if the blue arm line was removed, the blue hand on that arm and the red ball would also be erased. The player who removes the last line wins. I would highly recommend trying the game out for yourself: Play Red-Blue Hackenbush! I found after playing a few rounds it made a lot more sense.
| Figure 1: Hackenbush Girl |
As we have seen, Red-Blue Hackenbush clearly fulfills the requirements for a combinatorial game:
1. There are exactly two players (Left and Right).
2. No chance is involved.
3. Both players have perfect information.
4. Game is finite.
5. Someone must win, and the winner is determined by who makes the last move.
Who wins?
Under optimal play, we should be able to determine which player will win the game before they even begin. Let's start out with an easy example. Take a look at Figure 2 below. Who will win? |
| Figure 2: Girl and Boy |
As we can see, Left player has $14$ edges and Right player has $11$ edges. Left will win because they have $3$ more moves, $(14-11=3)$. So no matter who starts the game, Left will always win. Now this is an extremely simple game seeing as Lefts moves will not effect Rights moves and vice versa. Let's look at a bit trickier of an example in Figure 3.
 |
| Figure 3: Tweedledee and Tweedledum |
Zero Position: A position in which whoever starts the game will lose the game.
Fractional Moves
How do you determine the value of a move? In Figure 2: Girl and Boy, every move was worth an integer value. But some moves have fractional values. Let's take a look at Figure 4. |
| Figure 4: Half Moves |
What is the value of the position in Figure 4(a)? As you can see, no matter who goes first, Left will always win the game in 4a. But what happens when you add a red move of value $-1$. (Note: The value of moves are represented in terms of the value of the move to Left, so blue moves will be possitive, where red moves will be negative). As you can see in Figure 4(b), when a single red edge is added, Right will always win, no matter who goes first. So we know the value of the position in Figure 4(a), lets denote as $a$, must be $0<a<1$. In Figure 4(c), we finally have a zero game. After playing around, you will see that whoever goes first will lose. Now we know the value of the single red edge is $-1$ and we know the value of the game is $0$, so we know the value of $a$ can be determined by the equation $a+a-1=0$. Hence the value of the position $a$ is $\frac{1}{2}$.
What is the value of the position in Figure 4(d)? (Hint: whoever goes first will lose). That's right, you got it, Figure 4(d) is a zero position.
The value of particular moves can be difficult to determine and takes a lot of playing around with different scenarios. Figure 5 displays a table of already known values of certain positions.
 |
| Figure 5: Given Values of Hackenbush Positions |
Once you know the values of certain positions it becomes easier to determine the values of other positions. It is even easier if you know the game is a zero game. Let's take a look at Figure 6.
 |
| Figure 5: A Zero Game |
Determining the Value of a Hackenbush Games
 |
| Figure 6: Tree and Stump |
Examining the Hackenbush game in Figure 6. The tree has value $9$ and the stump has value $\frac{1}{2}$, so the entire position has value $9\frac{1}{2}$. Lets examine the possible moves. Right only has one move, and that is to a position of value $10$. The best move for Left would be to remove the blue edge of the stump, which would result in a position of value $9$.
The best move by Left is to move to a position of value $9$, the best move by Right is to move to position of value $10$. We can express this by the equation ${9|10}=9\frac{1}{2}$.
In general we have:
${n|n+1}=n+\frac{1}{2}$
${n| }=n+1$
${ | }=n+1$
${ |-n}=-(n+1)$
Simplicity Rule
Let v(G) represent the value of any Hackenbush position.Let b be the largest value of any position blue can move to.
Let r be the smallest value of any position red can move to.
Then
a.) There exist an integer $x$, such that $b<x<r$. So $v(G)$ will be the closes integer to zero.
If no such integer exist, then
b.) There exist a rational number, $x$, such that $b<x<r$ whose denominator is the smallest possible power of two.
Figure _ depicts possible b and r values. Try and determine the corresponding x value (without looking first).
 |
| Figure 7: Practice with Simplicity Rule |
Outcomes
Let $G$ represent the value of Hackenbush game.If $G>0$ Left wins.
If $G<0$ Right wins.
If $G=0$ the second player wins.
What's your Next Best Move?
When games get complicated it is not always easy to tell your best next move. Luckily we can use the binary number tree for that. Once you find the value of the position of your current game, you can find the value of the position you should move to in order to win. (This will make more sense when I explain in class).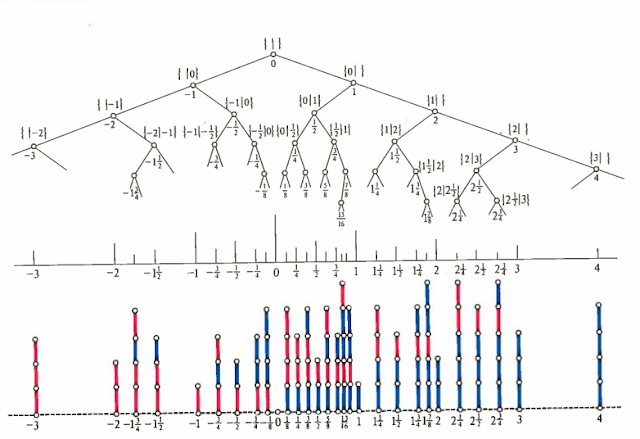 |
| Figure 8: Binary Number Tree |
Further Explorations
For this post I focused on Red-Blue Hackenbush. But there are numerous Hackenbush variations. Green Hackenbush is where all segments are green, and both players are allowed to choose any green segment. Red-Blue-Green Hackenbush is where there are red, green, and blue segments. Left player can choose any blue or green segments, while right player can choose any red or green segments. Although these seem like simple changes in the playing board, the effect on determining the best playing option is drastically different.
References
https://en.wikipedia.org/wiki/Hackenbushhttp://www-math.mit.edu/~rstan/transparencies/games.pdf
http://www.link.cs.cmu.edu/15859-s11/notes/Hackenbush.pdf
http://geometer.org/hackenbush/index.html
Game Theory, Thomas S. Ferguson
Winning Ways For Your Mathematical Plays, Volume 1, E.R. Berlekamp, J. H. Conway, R.K. Guy
Thanks for this interesting blog post Seneth. You're right- the game made a lot more sense to me after playing a few rounds of it, so thanks for providing the link to the game. The post was easy to follow and it seems like an interesting game to play. Finding the values of every move didn't make complete sense to me- specifically fractional values. I think after your presentation tomorrow and going through a few examples in class, I will understand it a lot better. I was also curious about whether this would work for a three person game (specifically the red-blue-green hackenbush), similarly to what we tested with Hex the other day. Overall, your post was really great!
ReplyDeleteThat would be interesting, and probably much more difficult, since a lot of Hackenbush strategy depends on the position values (and it's unclear how to compute that in 3 player versions). But here is a paper that talks about one kind of 3-player Hackenbush, which turns out to be very hard: http://www.iaeng.org/publication/IMECS2008/IMECS2008_pp226-230.pdf.
DeleteGreat use of the colored words. I too am having difficulty understanding the fractional move values, but I look forward to the presentation the rest of the post was easy to follow.
ReplyDeleteOne question I have: Does a zero position mean that whoever starts the game has to lose? Or is it similar to an P-position in that, assuming that the second player plays perfectly, it is impossible to win but still possible to win if the opponent messes up?
A zero-position is exactly like a P-position. From that position, the second person, under optimal play, can win.
DeleteThis comment has been removed by the author.
ReplyDeleteGreat post and presentation Seneth! This is a cool game that's fun to play, it was interesting to learn more about it. I am still a little confused about fractional moves, once you know the value of the position what do you do with that information? I guess i'm confused as to how it helps you, are you trying to get the value to 0?
ReplyDeleteThanks for your post and presentation Seneth! They were great! I enjoy playing this game a lot. However, I still feel a little bit confused about fractional moves. I think it makes sense to me when you presenting in class, but I get lost again when I playing alone after class. I guess I'm confused about the negative values and why in Figure 4(a) it must be the case that 0<a<1. Also, I'm curious about is it possible to play Red-Blue Hackenbush under misere rules? And is it possible to determine the winner if play it as a misere game? Again, this is an extremely interesting topic and thank you!
ReplyDeleteAmber
Seneth, your presentation was excellent! You seemed very comfortable with your topic in spite of the game's hidden intricacies. I definitely felt more qualified to play red-blue Hackenbush by the end of your presentation. Even so, I still think some of the fractional value calculations and use of the binary tree are beyond me. We established that positive fractional values and putting your opponent into a zero position give you an edge in the game-- that much I understand, but the rest....
ReplyDeleteI got to thinking about interesting variations of the game. I wonder what playing a non-partisan version of the game would be like? That is, what if all of the lines were the same color and each line was fair game for both players. That would obviously make for a quick and unsatisfying game, so you would have to set some kind of condition that limits the number of lines that can be taken in a single move. For example, what if you could take at most three connected lines, thus limiting the number of moves you could make and forcing players to play from top to bottom. I bet S-G would hold in this case because this variation of the game would be more Nim-ish.